luckcul's blog

越努力，越幸运

0%

Graph Embedding之node2vec

Posted on Edited on In

本文包括论文和源码细节

node2vec目标是训练比较通用的特征表示。将目标函数定义为与下游任务独立，以无监督的方式学习（和任务特定的训练方式得到的结果差别不明显）。使用点类型和边（是否存在）进行评估。

本论文是deepwalk工作的改进，主要改动为随机游走的策略，通过超参数控制BFS和DFS间的权衡。

Fuature Learning Framework

基础上还是使用了skip-gram结构，优化的目标函数:

$$max_f \sum_{u\in V}\log Pr(N_S(u) | f(u))$$

V是点集合，u是点，f(u)表示u的向量，$N_S(u)$表示通过策略S生成的邻居。为了易于训练，设定了两个假设：1）给定节点向量表示下周围邻居出现的概率是独立的，则

$$Pr(N_S(u) | f(u))=\prod_{n_i \in N_S(u)} Pr(n_i|f(u))$$

2)特征空间是对称的（问题：word2vec并不是这样，两个向量空间并没有共享？），则

$$P_r(n_i|f(u))=\frac{exp(f(n_i)\cdot f(u))}{\sum_{v\in V}exp(f(v)\cdot f(u))}$$

则，最开始的优化目标改写为：

$$max_f \sum_{v\in V} [ -log Z_u + \sum_{n_i\in N_S(u)}{f(n_i)\cdot f(u)} ]$$

其中 $Z_u=\sum_{v\in V} exp(f(u) \cdot f(v))$，（ps：这里应该还有一个因子$|N_S(u)|$ 常数），该部分直接计算量较大，可以使用负采样进行优化。

注意两个点：同质性（属于同一个社区）和同构性（结构相似），注意同构性不需要相连

Random Walks

从节点u开始随机游走l个节点，如果上一个节点为v，下一个节点x的概率为

$$P(c_i | c_{i-1}=v)= \begin{cases}
\frac{\pi_{vx}}{Z} \ if (v,x) \in E \ 0 \ otherwise
\end{cases}$$

具体的有偏的游走逻辑为：

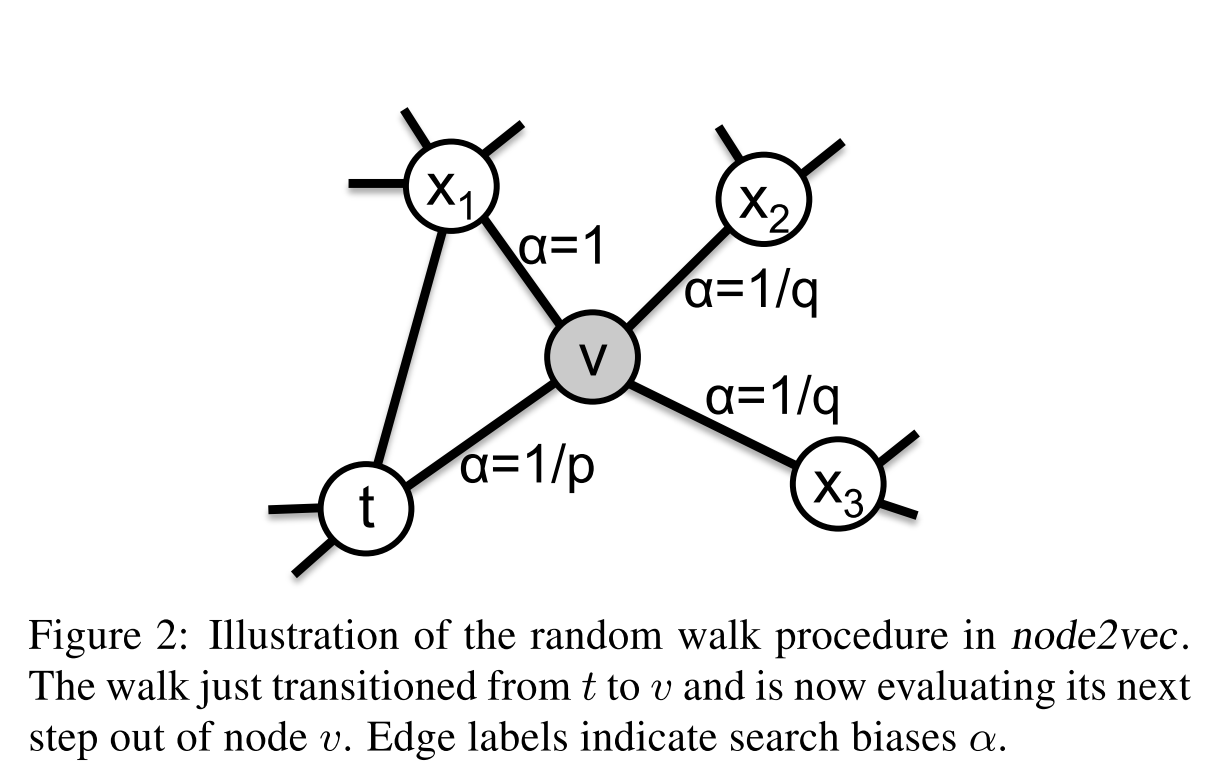
$$\alpha_{pq}(t,x) = \begin{cases} \frac{1}{p} \ if d_{tx} = 0 \ 1 \ if d_{tx} = 1 \ \frac{1}{q} \ if d_{tx} = 2 \end{cases}$$

当前节点为v，前一个节点为t，$d_{tx}$表示下一个节点x和上一个节点的距离。通过p、q两参数来权衡BFS和DFS策略（BFS更侧重学习结构化的特征、DFS更侧重学习社区化的特征）

https://res.cloudinary.com/dyhtzpcxp/image/upload/v1609085096/paper/node2vec/node2vec_randomwalk.png

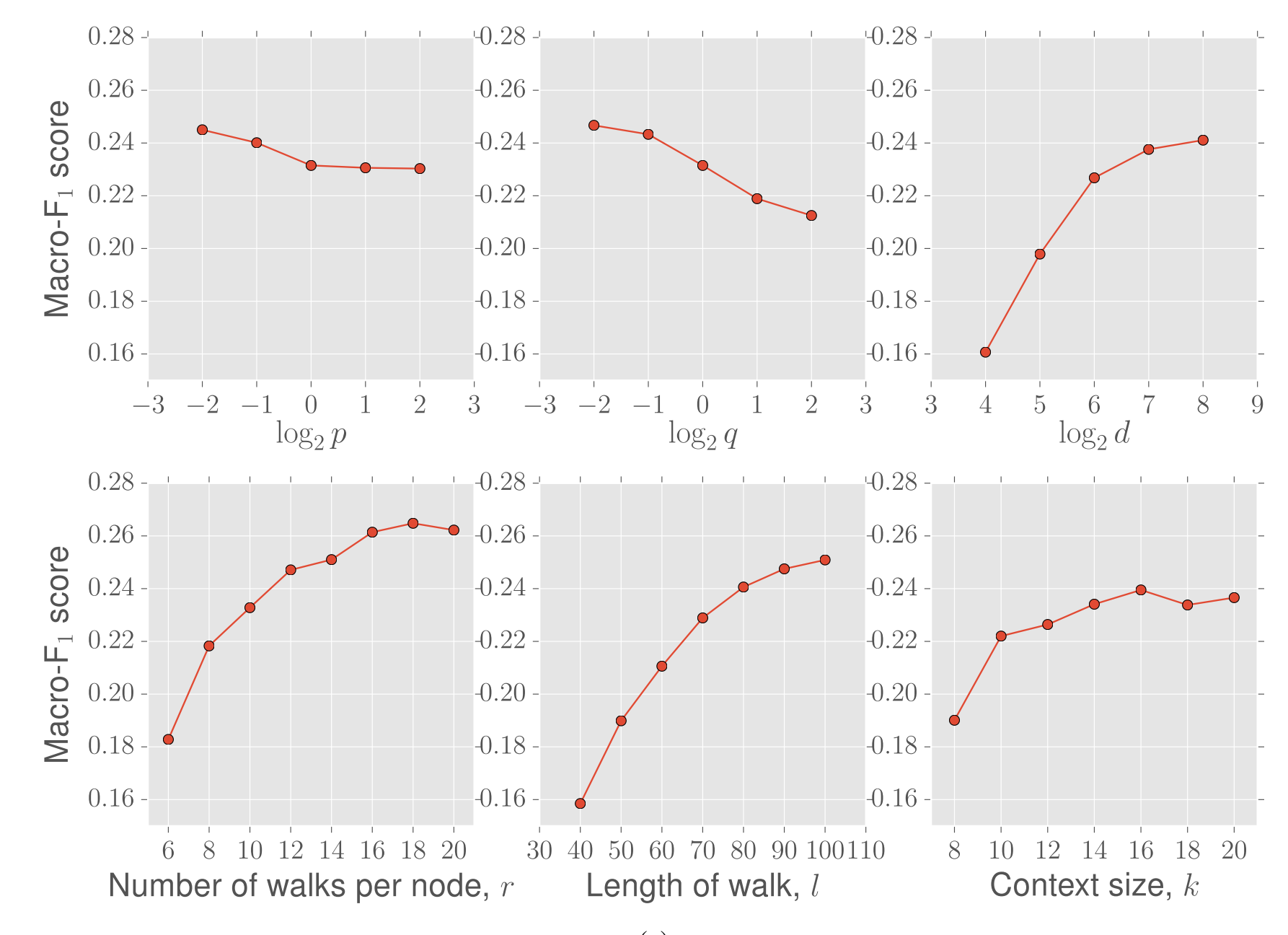
node2vec algorithm

算法逻辑如下，有几个超参数：r（每个节点的采样次数）、l（每个节点每次的采样步长）、k（skip-gram窗口大小）、p和q（随机游走参数）

https://res.cloudinary.com/dyhtzpcxp/image/upload/v1609085348/paper/node2vec/node2vec_algorithm.png

Experiments & Parameter

节点预测中，将学习得到的向量直接输入到one-vs-rest LR模型（L2正则）模型中进行分类。在可视化聚类用用的是k-means，p q 参数一般为$p,q \in {0.25, 0.5, 1, 2, 4}$。

向量维度在100以上增益不明显，窗口k在10以上增益不明显

https://res.cloudinary.com/dyhtzpcxp/image/upload/v1609085967/paper/node2vec/node2vec_parameter.png

源码

源码地址：https://github.com/aditya-grover/node2vec

使用networkx来维护图的数据结构，支持有向/无向图，支持带权/无权图。

skip-gram训练直接调用了gensim.models.Word2Vec ，代码的核心内容为使用随机游走构造训练集合。

构造训练集主要分两部分，第一部分是打表，先计算每个点下一步随机游走概率的中间结果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
def preprocess_transition_probs(self):
    '''
    Preprocessing of transition probabilities for guiding the random walks.
    '''
    G = self.G
    is_directed = self.is_directed

    alias_nodes = {}
		# 处理单节点（用以起点的随机游走）
    for node in G.nodes():
        unnormalized_probs = [G[node][nbr]['weight'] for nbr in sorted(G.neighbors(node))]
        norm_const = sum(unnormalized_probs)
        normalized_probs =  [float(u_prob)/norm_const for u_prob in unnormalized_probs]
        alias_nodes[node] = alias_setup(normalized_probs)

    alias_edges = {}
    triads = {}
		# 处理双节点（用以已知上一节点的随机游走）
    if is_directed:
        for edge in G.edges():
            alias_edges[edge] = self.get_alias_edge(edge[0], edge[1])
    else:
        for edge in G.edges():
            alias_edges[edge] = self.get_alias_edge(edge[0], edge[1])
            alias_edges[(edge[1], edge[0])] = self.get_alias_edge(edge[1], edge[0])

    self.alias_nodes = alias_nodes
    self.alias_edges = alias_edges

    return

其中核心的是的是alias_setup 函数（实现了Alias算法），详解见这里。这是一种复杂度O(1)的采样算法，如果不用这种方式，需要每次生成随机数，然后O(n)或O(log(n))的复杂度进行生成，效率较低。对于一组离散输入的概率，返回J（每个位置和另一个位置），q（当前的概率值）。ps：查询时生成两个随机数即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
def alias_setup(probs):
	'''
	Compute utility lists for non-uniform sampling from discrete distributions.
	Refer to https://hips.seas.harvard.edu/blog/2013/03/03/the-alias-method-efficient-sampling-with-many-discrete-outcomes/
	for details
	'''
	K = len(probs)
	q = np.zeros(K)
	J = np.zeros(K, dtype=np.int)

	smaller = []
	larger = []
	for kk, prob in enumerate(probs):
	    q[kk] = K*prob
	    if q[kk] < 1.0:
	        smaller.append(kk)
	    else:
	        larger.append(kk)

	while len(smaller) > 0 and len(larger) > 0:
	    small = smaller.pop()
	    large = larger.pop()

	    J[small] = large
	    q[large] = q[large] + q[small] - 1.0
	    if q[large] < 1.0:
	        smaller.append(large)
	    else:
	        larger.append(large)

	return J, q

第二部分，随机游走（基于前面的打表结果）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def simulate_walks(self, num_walks, walk_length):
		'''
		Repeatedly simulate random walks from each node.
		'''
		G = self.G
		walks = []
		nodes = list(G.nodes())
		print 'Walk iteration:'
		for walk_iter in range(num_walks): # 游走轮数
			print str(walk_iter+1), '/', str(num_walks)
			random.shuffle(nodes)
			for node in nodes:#对每个点游走walk_length次
				walks.append(self.node2vec_walk(walk_length=walk_length, start_node=node))

		return walks

单次游走

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
def node2vec_walk(self, walk_length, start_node):
		'''
		Simulate a random walk starting from start node.
		'''
		G = self.G
		alias_nodes = self.alias_nodes
		alias_edges = self.alias_edges

		walk = [start_node]

		while len(walk) < walk_length:
			cur = walk[-1]
			cur_nbrs = sorted(G.neighbors(cur))
			if len(cur_nbrs) > 0:
				if len(walk) == 1:
					walk.append(cur_nbrs[alias_draw(alias_nodes[cur][0], alias_nodes[cur][1])])
				else:
					prev = walk[-2]
					next = cur_nbrs[alias_draw(alias_edges[(prev, cur)][0], 
						alias_edges[(prev, cur)][1])]
					walk.append(next)
			else:
				break

		return walk

reference